
Once you’ve accepted that Pac Man takes place on a torus
you can extend the same trick to make higher-genus manifolds.

Once you’ve accepted that Pac Man takes place on a torus
you can extend the same trick to make higher-genus manifolds.
OK, not every day. But whenever I shop for packaged retail goods like a coffee or in the grocers.
The Pythagorean theorem demonstrates that a slightly larger circle has twice as much area as a slightly smaller circle.
(Since the diagonal of that square is √2 long relative to the “1” of the interior radius=leg of the right triangle. So the outer radius=hypotenuse=√2, and √2 squared is 2.)
And some of us know from Volume Integrals in calculus class that a cylinder's volume = circle area × height — and something like a sausage with a fat middle, or a cup with a wider mouth than base, can be thought of as a “stack” of circle areas
or in the case of a tapered glass, a “rectangle minus triangle” (when the circle is collapsed so just looking at base-versus-height “camera straight ahead on the table” view).

The shell-or-washer-method volume integral lessons were, I think, supposed to teach about symbolic manipulation, but I got a sense of what shapes turn out to be big or small volume as well.
By integrating dheight sized slices of circles that make up a larger 3-D shape, I can apply the inverse-square lesson of the Pythagorean theorem to how real-life “cylinders” or “cylinder-like things” will compare in volume.



16 pages for non-brainiacs on the Hopf fibration by David Lyons
S³→S²ƒ(a,b,c,d) = (a²+b²−c²−d²,,)S³→S²ƒ[a,b,c,d] = [a²+b²−c²−d²,2(ad+bc),2(bd−ac)]Gimbal lock, composition of rotation maps


to get the general three-angle rotation group
but this is ugly and wrong—not because there are too many trig words, but because if you play around with it enough you’ll see that—just like the North Pole and South Pole have redundant longitude coordinates—various combinations of [phi;,theta;,psi;] can overlap each other or even get caught in a Gimbal Lock.










A noncommutative space (picture by Lieven Le Bruyn)

Monotone and antitone functions
(not over ℝ just the domain you see = 0<x<1⊂ℝ)
These are examples of invertible functions.
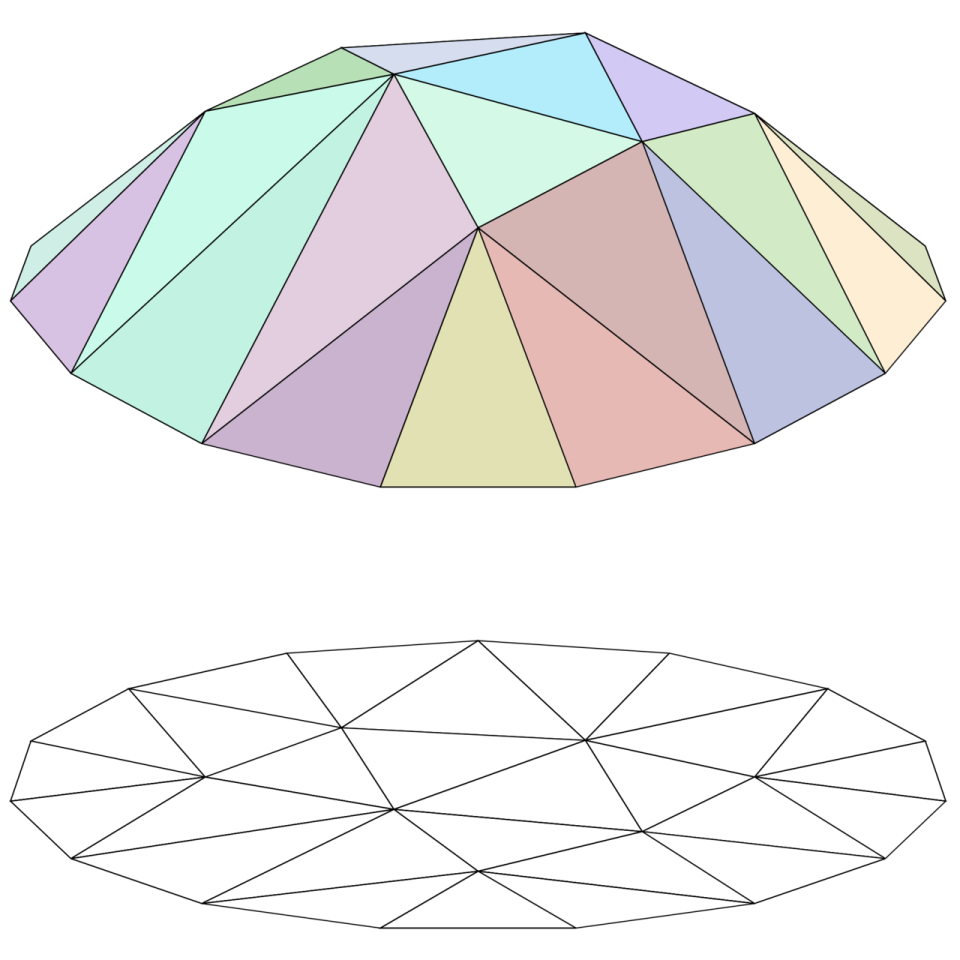
A piecewise linear function in two dimensions (top) and the convex polytopes on which it is linear (bottom).

Cylinder = line-segment × disc
C = | × ●
The “product rule” from calculus works as well with the boundary operator ∂ as with the differentiation operator ∂.
∂C = ∂| × ● + | × ∂●



>Oops. Typo. Sorry, I did this really late at night! cos and sin need to be swapped back.









Oops. Another typo. Wrong formula for circumference.


Distribution of primes up to 19# (9699690).
Further along my claim that what separates mathematicians from everyone else is:
and that learning 20th-century geometry might expand your imagination beyond the usual impoverished shapes of taxonomies.
Here are some calisthenics you can do with a pen and paper that I hope give you a feel for what a (mathematical) group is. (It’s a shame that “group”, “set”, “class”, “category”, “bundle” all have distinct meanings within mathematics. Another part of the language barrier.)
Think of “a group” this way. A group catalogues the relationships between “verbs”.
That is: think of a function as a “verb” and the thing it operates on as a “noun”. One of the tricks of abstraction is that these can be interchanged. Maybe what that might mean will already come clear from this example.

Starting with a pentagon, which I’ll just represent with five numbers for the points. (So: whatever works here might work on other “circles of five”—or “decks of 52”—or … something else you come up with!) That will be the one “thing” or “noun” and in the group exploration you’ll see that the “structure of the verbs” is more interesting than whatever they’re acting on. (This is why in group theory the name of the object is usually omitted and people just list the operations/verbs.)

In John Baez’s week62 you can read about reflection groups. I picked two “axes” in my pentagon ⬟ arbitrarily. If you’re writing along you can draw a different -gon or different axes. Reflection is going to mean interchanging numbers across the axis (“mirror”).



It’s the same as reflecting the Mona Lisa except you don’t have to re paint the portrait every time. The same 2-dimensional plane can be indexed by the numbers more easily than by the whole image. (Unless you’re following along with computer tools and you’ve chosen “the square” as your shape. Then transforming Mona is probably more interesting.)

Without my saying so it’s probably obvious that reflecting twice would bring you back to the start. Flip Mona upside-down, flip the pentagon ⬟ along a, then repeat.

If you wanted to give “starting point of noun” a verb-name you could just say 1•noun.
What that establishes, formulaically, is that ƒ(ƒ(X))=X (where X is Mona or ⬟). Where ƒ is “flip”. We’ve also established that ƒ=ƒ⁻¹. Trivial observation, maybe-not-trivial in formula form! After all, suppose you had some science problem and it included a long sequence of ƒ(g(ƒ(ƒ(ƒ(h(g(X))))))) type stuff. You could make it shorter (and maybe the resulting formula or computation easier) if you could cancel ƒƒ’s like that.
That works for either of my pentagon ⬟ reflections a(⬟) or b(⬟).
a(a(⬟))=⬟ andb(b(⬟))=⬟.
What group theory is going to talk about is how the two verbs interact. What happens when I do a(a(b(a(b(⬟))))) ? Well I can already simplify it by reducing any trains of a∘a∘a∘a’s or b∘b∘b’s.

Above are the first few results of a∘b∘a[⬟]. (NB: “The first” operation is on the right since the thing it’s acting on only appears all the way to the right. So in group theory we have to read right-to-left ←.) I’ll write a bit more text for those who want to continue the chain on their own to give you time to look away. You could also try doing b∘a∘b[⬟] where I did a∘b∘a[⬟] (read right to left! ←).
Just like it’s “sort of amazing” in some sense that
So is it also a bit amazing that maybe these reflection laws will be order-invariant in some sense as well.
That may seem like less big of a deal if you think “Everything in maths is commutative and symmetrical”—but it’s not! And most things in life are not commutative or symmetrical. Try to drink your milk and then pour it into the glass or don your underwear after your pants.

It’s also not so obvious (if nobody had told you the answer first and you just had to figure it out yourself) that b∘a∘b∘a∘b∘a∘b∘a∘b∘a[⬟] = ⬟.![b∘a∘b∘a∘b∘a∘b∘a∘b∘a[⬟]](https://i0.wp.com/media.tumblr.com/d4f0580b8ad486a109a163303399f6ab/tumblr_inline_mk6xaqbZ6Q1qbdydv.png)
Another fairly easy shape to explore its groups is the square. (And what goes for the square, goes for the plane 𝔸²—or for 1-dimensional complex numbers ℂ.)



That’s the end of what a group is. Next: looking ahead to put them in context.
All of these activities amount to exploring the building blocks of a particular group.
But someone (Arthur Cayley) has also come up with a good way to look at the entire structure of the verbs.

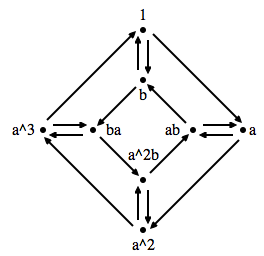

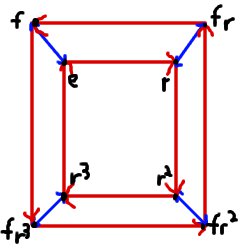







.png)

Which is ultimately where this theory wants to go: to help us compare & contrast verb-structures. (Look up “group homomorphism”.) Or to notice that two natural phenomena exhibit the same verb-structure.
You can download a free program called Group Explorer to look at various Cayley diagrams.


In an upcoming post called The Shape of Logic, the Logic of Shape I’ll talk about the relationship between groups and manifolds.

Where I’ll ultimately want to go with this is to call groups a “periodic table of elements” for logic. That may not be exact but it’s a gist. Given that semigroups, groups, Lie groups, and other assumption-swapped variations on the group concept usually turn out to be “Factorable” into simple components (Jordan-Hölder, Krohn-Rhodes, etc.)—and assuming that the Universe somehow builds itself out of primitives sufficiently determined or governed by mathematics—or at the least, that normal people can learn this periodic table and expand their imagination with powers of 20th century geometry.
John Baez:
“There must be hundreds of mathematicians roaming the earth thinking operads are difficult and abstruse, because they’ve seen the definition without any pictures.
These people should be grateful they weren’t taught how to tie their shoes in an equally wrong-headed manner.”
What is an operad?
Why should someone interested in homotopy care about operads?