one can basically describe each of the classical geometries (Euclidean, affine, projective,spherical, hyperbolic, Minkowski, etc.) as a homogeneous space for its structure group.

The structure group (or gauge group) of the class of geometric objects arises from isomorphisms of one geometric object to the standard object of its class.

For example,

• • the structure group for lengths is ℝ⁺;
• the structure group for angles is ℤ/2ℤ;
• the structure group for lines is the affine group Aff(ℝ);
• the structure group for n-dimensional Euclidean geometry is the Euclidean group E(n);
• • the structure group for oriented 2-spheres is the (special) orthogonal group SO(3).

Terence Tao

(I rearranged his text freely.)

What is group theory?

Further along my claim that what separates mathematicians from everyone else is:

• matrices
• groups
• manifolds

and that learning 20th-century geometry might expand your imagination beyond the usual impoverished shapes of taxonomies.

Here are some calisthenics you can do with a pen and paper that I hope give you a feel for what a (mathematical) group is. (It’s a shame that “group”, “set”, “class”, “category”, “bundle” all have distinct meanings within mathematics. Another part of the language barrier.)

Think of “a group” this way. A group catalogues the relationships between “verbs”.

That is: think of a function as a “verb” and the thing it operates on as a “noun”. One of the tricks of abstraction is that these can be interchanged. Maybe what that might mean will already come clear from this example.

Starting with a pentagon, which I’ll just represent with five numbers for the points. (So: whatever works here might work on other “circles of five”—or “decks of 52”—or … something else you come up with!) That will be the one “thing” or “noun” and in the group exploration you’ll see that the “structure of the verbs” is more interesting than whatever they’re acting on. (This is why in group theory the name of the object is usually omitted and people just list the operations/verbs.)

In John Baez’s week62 you can read about reflection groups. I picked two “axes” in my pentagon ⬟ arbitrarily. If you’re writing along you can draw a different -gon or different axes. Reflection is going to mean interchanging numbers across the axis (“mirror”).

It’s the same as reflecting the Mona Lisa except you don’t have to re paint the portrait every time. The same 2-dimensional plane can be indexed by the numbers more easily than by the whole image. (Unless you’re following along with computer tools and you’ve chosen “the square” as your shape. Then transforming Mona is probably more interesting.)

Without my saying so it’s probably obvious that reflecting twice would bring you back to the start. Flip Mona upside-down, flip the pentagon ⬟ along a, then repeat.

If you wanted to give “starting point of noun” a verb-name you could just say 1•noun.

What that establishes, formulaically, is that ƒ(ƒ(X))=X (where X is Mona or ⬟). Where ƒ is “flip”. We’ve also established that ƒ=ƒ⁻¹. Trivial observation, maybe-not-trivial in formula form! After all, suppose you had some science problem and it included a long sequence of ƒ(g(ƒ(ƒ(ƒ(h(g(X))))))) type stuff. You could make it shorter (and maybe the resulting formula or computation easier) if you could cancel ƒƒ’s like that.

That works for either of my pentagon ⬟ reflections a(⬟) or b(⬟).

• a(a(⬟))=⬟ and
• b(b(⬟))=⬟.

What group theory is going to talk about is how the two verbs interact. What happens when I do a(a(b(a(b(⬟))))) ? Well I can already simplify it by reducing any trains of a∘a∘a∘a’s or b∘b∘b’s.

Above are the first few results of a∘b∘a[⬟]. (NB: “The first” operation is on the right since the thing it’s acting on only appears all the way to the right. So in group theory we have to read right-to-left ←.) I’ll write a bit more text for those who want to continue the chain on their own to give you time to look away. You could also try doing b∘a∘b[⬟] where I did a∘b∘a[⬟] (read right to left! ←).

Just like it’s “sort of amazing” in some sense that

1. •••—•••—•••—••• (four groups of three…um, regular meaning of “group”!) is the same as ••••—••••—•••• (three groups of four)…and that not only in this specific case but we could make a “law” out of it

So is it also a bit amazing that maybe these reflection laws will be order-invariant in some sense as well.

That may seem like less big of a deal if you think “Everything in maths is commutative and symmetrical”—but it’s not! And most things in life are not commutative or symmetrical. Try to drink your milk and then pour it into the glass or don your underwear after your pants.

It’s also not so obvious (if nobody had told you the answer first and you just had to figure it out yourself) that b∘a∘b∘a∘b∘a∘b∘a∘b∘a[⬟] = ⬟.
 

Another fairly easy shape to explore its groups is the square. (And what goes for the square, goes for the plane 𝔸²—or for 1-dimensional complex numbers ℂ.)

That’s the end of what a group is. Next: looking ahead to put them in context.

All of these activities amount to exploring the building blocks of a particular group.

But someone (Arthur Cayley) has also come up with a good way to look at the entire structure of the verbs.

   

Which is ultimately where this theory wants to go: to help us compare & contrast verb-structures. (Look up “group homomorphism”.) Or to notice that two natural phenomena exhibit the same verb-structure.

You can download a free program called Group Explorer to look at various Cayley diagrams.

In an upcoming post called The Shape of Logic, the Logic of Shape I’ll talk about the relationship between groups and manifolds.

Where I’ll ultimately want to go with this is to call groups a “periodic table of elements” for logic. That may not be exact but it’s a gist. Given that semigroups, groups, Lie groups, and other assumption-swapped variations on the group concept usually turn out to be “Factorable” into simple components (Jordan-Hölder, Krohn-Rhodes, etc.)—and assuming that the Universe somehow builds itself out of primitives sufficiently determined or governed by mathematics—or at the least, that normal people can learn this periodic table and expand their imagination with powers of 20th century geometry.

Automorphisms

We want to take theories and turn them over and over in our hands, turn the pants inside out and look at the sewing; hold them upside down; see things from every angle; and sometimes, to quotient or equivalence-class over some property to either consider a subset of cases for which a conclusion can be drawn (e.g., “all fair economic transactions” (non-exploitive?) or “all supply-demand curveses such that how much you get paid is in proportion to how much you contributed” (how to define it? vary the S or the D and get a local proportionality of PS:TS? how to vary them?)

Consider abstractly a set like {a, b, c, d}. 4! ways to rearrange the letters. Since sets are unordered we could call it as well the quotient of all rearangements of quadruples of once-and-yes-used letters (b,d,c,a). /p>

Descartes’ concept of a mapping is “to assign” (although it’s not specified who is doing the assigning; just some categorical/universal ellipsis of agency) members of one set to members of another set.

• For example the Hash Map of programming.

  {
   '_why' => 'famous programmer',
   'North Dakota' => 'cold place',
   ... }

• Or to round up ⌈num⌉: not injective because many decimals are written onto the same integer.

  

  

• Or to “multiply by zero” i.e. “erase” or “throw everything away”:

Old programmers don’t die, they’re piped to /dev/null.

— protea (@isomorphisms) January 2, 2013

Linear maps with det=0 :: - | /dev/null :: matter into a black hole :: (or, on Earth, a trash grinder)

— protea (@isomorphisms) January 2, 2013

In this sense a bijection from the same domain to itself is simply a different—but equivalent—way of looking at the same thing. I could rename A=1,B=2,C=3,D=4 or rename A='Elsa',B='Baobab',C=√5,D=Hypathia and end with the same conclusion or “same structure”. For example. But beyond renamings we are also interested in different ways of fitting the puzzle pieces together. The green triangle of the wooden block puzzle could fit in three rotations (or is it six rotations? or infinity right-or-left-rotations?) into the same hole.

By considering all such mappings, dividing them up, focussing on the easier classes; classifying the types at all; finding (or imposing) order|pattern on what seems too chaotic or hard to predict (viz, economics) more clarity or at least less stupidity might be found.

The hope isn’t completely without support either: Quine explained what is a number with an equivalence class of sets; Tymoczko described the space of musical chords with a quotient of a manifold; PDE’s (read: practical engineering application) solved or better geometrically understood with bijections; Gauss added 1+2+3+...+99+100 in two easy steps rather than ninety-nine with a bijection; ….

It’s hard for me to speak to why we want groups and what they are both at once. Today I felt more capable of writing what they are.

So this is the concept of sameness, let’s discuss just linear planes (or, hyperplanes) and countable sets of individual things.

Leave it up to you or for me later, to enumerate the things from life or the physical world that “look like” these pure mathematical things, and are therefore amenable by metaphor and application of proved results, to the group theory.

But just as one motivating example: it doesn’t matter whether I call my coordinates in the mechanical world of physics (x,y,z) or (y,x,z). This is just a renaming or bijection from {1,2,3} onto itself.

Even more, I could orient the axis any way that I want. As long as the three are mutually perpendicular each to the other, the origin can be anywhere (invariance under an affine mapping — we can equivalence-class those together) and the rotation of the 3-D system can be anything. Stand in front of the class as the teacher, upside down, oriented so that one of the dimensions helpfully disappears as you fly straight forward (or two dimensions disappear as you run straight forward on a flat road). Which is an observation taken for granted by my 8th grade physics teacher. But in the language of group theory means we can equivalence-class over the special linear group of 3-by-3 matrices that leave volume the same. Any rotation in 3-D

Sameness-preserving Groups partition into:

• permutation groups, or rearrangements of countable things, and
• linear groups, or “trivial” “unimportant” “invariant” changes to continua (such as rescaling—if we added a “0” to the end of all your currency nothing would change)
  
• conjunctions of smaller groups

The linear groups—get ready for it—can all be represented as matrices! This is why matrices are considered mathematically “important”. Because we have already conceived this huge logical primitive that (in part) explains the Universe (groups) — or at least allows us to quotient away large classes of phenomena — and it’s reducible to something that’s completely understood! Namely, matrices with entries coming from corpora (fields).

So if you can classify (bonus if human beings can understand the classification in intuitive ways) all the qualitatively different types of Matrices,

then you not only know where your engineering numerical computation is going, but you have understood something fundamental about the logical primitives of the Universe!

Aaaaaand, matrices can be computed on this fantastic invention called a computer!

unf

differential topology lecture by John W. Milnor from the 1960’s: Topology from the Differentiable Viewpoint

• A function that’s problematic for analytic continuations:
  
  
• Definitions of smooth manifold, diffeomorphism, category of smooth manifolds
• bicontinuity condition
• two Euclidean spaces are diffeomorphic iff they have the same dimension
• torus ≠ sphere but compact manifolds are equivalence-classable by genus
• Moebius band is not compact
• Four categories of topology, which were at first thought to be the same, but by the 60’s seen to be really different (and the maps that keep you within the same category):
  
  diffeomorphisms on smooth manifolds;
  
  

  
  

  piecewise-linear maps on simplicial complexes;
  
  
  
  
  homeomorphisms on sets (point-set topology)
  

  

  
  

• Those three examples of categories helped understand category and functor in general. You could work for your whole career in one category—for example if you work on fluid dynamics, you’re doing fundamentally different stuff than computer scientists on type theory—and this would filter through to your vocabulary and the assumptions you take for granted. Eg “maps” might mean “smooth bicontinuous maps” in fluid dynamics but non-surjective, discontinuous maps are possible all the time in logic or theoretical comptuer science. Functor being the comparison between the different subjects.
• The fourth, homotopy theory, was invented in the 1930’s because topology itself was too hard.

  

• Minute 38-40. A pretty slick proof. I often have a hard time following, but this is an exception.
• Minute 43. He misspeaks! In defining the hypercube.
• Minute 47. Homology groups relate the category of topological-spaces-with-homotopy-classes-of-mappings, to the category of groups-with-homomorphisms.

That’s the first of three lectures. Also Milnor’s thoughts almost half a century later on how differential topology had evolved since the lectures:

Hat tip to david a edwards.

What I really loved about this talk was the categorical perspective. The talks are really structured so that three categories — smooth things, piecewise things, and points/sets — are developed in parallel. Better than development of the theory of categories in the abstract, I like having these specific examples of categories and how “sameness” differs from category to category.

(Source: http://player.vimeo.com/)

An Ugly Discontinuity II

Here’s another example of what mathematicians mean by an “ugly discontinuity”.

The Torus is the Cartesian product of circles ◯×◯. I.e. an abstract geometry in which concrete angular measurement pairs (or triples or quadruples or quintuples or …) are realised.

The Sphere is … not that.

It’s nontrivial to recognise that ◯×◯≠sphere. For example the people who wrote the Starfox battle mode drew the screen as a sphere but programmed the battle mode on a torus.

By the Hairy Ball Theorem we know that spheres are different to independent pairs of circles. Specifically: one circle “vanishes” at the top and bottom of the other, to make a sphere. Changing your latitude coordinate at the North Pole  leaves you in the same place. In other words “two” collapses to “one” at the poles which also implies that, for consistency, latitude needs to be close to collapse around 89°N—not at all like ◯×◯. where the two capstans spin freely independent of one another.

(This is half of the “joke” … or, “prank”, or “not-funny joke” in my twitter location. I designate myself at (−90,45) so you can imagine a person spinning around uselessly as they try to “walk in a circle” on the South Pole. OK … it’s only slightly funny even to me.)

This is like how globes can represent the Earth much better than maps on a flat sheet of paper. Since it’s impossible to map R² onto S², flat maps can never be perfect. (The fact that the difference is merely a point—that is R² does map onto S²{0}—is a distraction from how distorted real maps get. Look how different Greenland looks from the North versus the European view

Furthermore the torus can’t be deformed into a sphere, and it’s difficult for mathematicians to see the relationships between high-dimensional and low-dimensional spheres. (And this has something to do with the story of what Grigory Perelman achieved in solving that Clay Prize.)

The savvy way of talking about this is to say that the sphere has ugly symmetries. How can I say that when the Sphere is a Platonically perfect elementary shape?! The Sphere is so perfect that mass in outer space likes to form itself into that most balanced of balanced shapes.

//

Basically because when you hold the globe with two fingers and your friend spins it, the antipodes where your two fingers are holding it don’t move. (Yes, neighbourhoods around them move—but “points” in the infinitely-deep-down-continuum-set-of-measure-zero sense are singularities (erm, singularities in the 1/z sense, not in the “black hole” sense).)

Tomorrow: a post on a statistical application of the humble circle.

∄ inverse

• I cheated on you. ∄ way to restore the original pure trust of our early relationship.
• The broken glass. Even with glue we couldn’t put it back to be the same original glass.
• I got old. ∄ potion to restore my lost youth.
• Adam & Eve ate from the tree of the knowledge of good & evil. They could not unlearn what they learned.
• “Be … careful what you put in that head because you will never, ever get it out.” ― Thomas Cardinal Wolsey
• We polluted the lake with our sewage runoff. The algal blooms choked off the fish. ∄ way to restore it.
• Phase change. And the phase boundary can only be traversed one direction (or the backwards direction costs vastly more energy). The marble rolls off the table, the leg poisoned by gangrene. The father dies at war. The unkind words can’t be unsaid.

#semigroups

Primitives

I guess when most people hear the word “logic”, they think of

• cold shoulders
• loveless robots
• a not-quite-rational preoccupation with principles, propositions, facts, and categorical truths over people, feelings, subjective impressions
  
• making the wrong decision by thinking in straight lines
  
  
  

  instead of reaction clouds and propagation networks and games and what-he-thinks-she-thinks-I-know and things that swirl or squish
  

But when I hear the word “logic”, I think of

• the beautiful scrivenings of academics who have worked out the shapes of network relations, time & causality, Boolean algebra; untangled modality and self-reference;
• the complete classification of all finite simple groups. This is a feat so massive that I have trouble describing its hugeness. It’s like, we pathetic worms called human beings have uncovered something real and unerring and definite and complete about the Universe. Not just our universe, but any possible universe. We’ve uncovered laws that constrain even G–d.
• I remember looking out over a field of grasses wavering in the wind, a vector field billowing like waves of water, and thinking back on a talk by Stephen Wolfram.
  
  Everything is computation, he said. I saw in my mind’s eye the bits of wind and of grass digitised—not necessarily in Q*bert blocks,
  
  but in a dynamic and skeletal topology.
  
  
  
  Conway’s Game of Life
  
  
  
  playing out at a femto scale—the bits of air blowing on the bits of grain, the grains reacting back; the chromoclouds dynamically crunching their numbers in Douglas Noël Adams’ Monte Carlo simulation to compute the question whose answer is 42; the photo-rods −ct of timespace digitally passing into my retina, lighting off neural logics;
  
  

  muscles contracting only at the micro scale because their chemical pathways each consist of thousands of nanoscale back-and-forths;
  
  

  phospholipid cell-walls digitally repelling or allowing the chemicals for the micro breathers that make me up (and yet don’t—fuzzy logic? help?)

• in short, Logic as the Hand of G-d, making everything in the Universe.

If God speaks to man, he undoubtedly uses the language of mathematics.

—Henri Poincaré

,An exposition of the first isomorphism theorem using horsies and doggies … well, cows, at least.

by Tim Sullivan

(Source: https://docs.google.com/)

A road map of mathematical objects by Max Tegmark, via intothecontinuum:

The arrows generally indicate addition of new symbols and/or axioms. Arrows that meet indicate the combination of structures.

For instance, an algebra is a vector space that is also a ring, and a Lie group is a group that is also a manifold.

How do I Create the Identity Matrix in R? Also a bit of group theory.

I googled for this once upon a time and nothing came up. Hopefully this saves someone ten minutes of digging about in the documentation.

You make identity matrices with the keyword diag, and the number of dimensions in parentheses.

> diag(3)
     [,1] [,2] [,3]
[1,]    1 0 0
[2,]    0 1 0
[3,]    0 0 1 

That’s it.

> diag(11)
      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
 [1,]    1 0 0 0 0 0 0 0 0 0 0
 [2,]    0 1 0 0 0 0 0 0 0 0 0
 [3,]    0 0 1 0 0 0 0 0 0 0 0
 [4,]    0 0 0 1 0 0 0 0 0 0 0
 [5,]    0 0 0 0 1 0 0 0 0 0 0
 [6,]    0 0 0 0 0 1 0 0 0 0 0
 [7,]    0 0 0 0 0 0 1 0 0 0 0
 [8,]    0 0 0 0 0 0 0 1 0 0 0
 [9,]    0 0 0 0 0 0 0 0 1 0 0
[10,]    0 0 0 0 0 0 0 0 0 1 0
[11,]    0 0 0 0 0 0 0 0 0 0 1 

But while I have your attention, let’s do a couple mathematically interesting things with identity matrices.

First of all you may have heard of Tikhonov regularisation, or ridge regression. That’s a form of penalty to rule out overly complex statistical models. @benoithamelin explains on @johndcook’s blog that

• Tikhonov regularisation is also a way of puffing air on a singular matrix det|M|=0 so as to make the matrix invertible without altering the eigenvalues too much.

Now how about a connection to group theory?

First take a 7-dimensional identity matrix, then rotate one of the rows off the top to the bottom row.

> diag(7)[ c(2:7,1), ]
     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,]    0 1 0 0 0 0 0
[2,]    0 0 1 0 0 0 0
[3,]    0 0 0 1 0 0 0
[4,]    0 0 0 0 1 0 0
[5,]    0 0 0 0 0 1 0
[6,]    0 0 0 0 0 0 1
[7,]    1 0 0 0 0 0 0 

Inside the brackets it’s [row,column]. So the concatenated c(2,3,4,5,6,7,1) become the new row numbers.

Let’s call this matrix M.7 (a valid name in R) and look at the multiples of it. Matrix multiplication in R is the %*% symbol, not the * symbol. (* does entry-by-entry multiplication, which is good for convolution but not for this.)

Look what happens when you multiply M.7 by itself: it starts to cascade.

> M.7   %*%   M.7
     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,]    0 0 1 0 0 0 0
[2,]    0 0 0 1 0 0 0
[3,]    0 0 0 0 1 0 0
[4,]    0 0 0 0 0 1 0
[5,]    0 0 0 0 0 0 1
[6,]    1 0 0 0 0 0 0
[7,]    0 1 0 0 0 0 0


> M.7   %*%   M.7   %*%   M.7
     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,]    0 0 0 1 0 0 0
[2,]    0 0 0 0 1 0 0
[3,]    0 0 0 0 0 1 0
[4,]    0 0 0 0 0 0 1
[5,]    1 0 0 0 0 0 0
[6,]    0 1 0 0 0 0 0
[7,]    0 0 1 0 0 0 0 

If I wanted to do straight-up matrix powers rather than typing M %*% M %*% M %*% M %*% ... %*% M 131 times, I would need to require(expm) package and then the %^% operator for the power.

Here are some more powers of M.7:

> M.7   %^%   4
     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,]    0 0 0 0 1 0 0
[2,]    0 0 0 0 0 1 0
[3,]    0 0 0 0 0 0 1
[4,]    1    0    0    0    0    0    0
[5,]    0    1    0    0    0    0    0
[6,]    0    0    1    0    0    0    0
[7,]    0    0    0    1    0    0    0


> M.7   %^%   5
     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,]    0 0 0 0 0 1 0
[2,]    0 0 0 0 0 0 1
[3,]    1    0    0    0    0    0    0
[4,]    0    1    0    0    0    0    0
[5,]    0    0    1    0    0    0    0
[6,]    0    0    0    1    0    0    0
[7,]    0    0    0    0    1    0    0


> M.7   %^%   6
     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,]    0 0 0 0 0 0 1
[2,]    1    0    0    0    0    0    0
[3,]    0    1    0    0    0    0    0
[4,]    0    0    1    0    0    0    0
[5,]    0    0    0    1    0    0    0
[6,]    0    0    0    0    1    0    0
[7,]    0    0    0    0    0    1    0


> M.7   %^%   7
     [,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,]    1    0    0    0    0    0    0
[2,]    0    1    0    0    0    0    0
[3,]    0    0    1    0    0    0    0
[4,]    0    0    0    1    0    0    0
[5,]    0    0    0    0    1    0    0
[6,]    0    0    0    0    0    1    0
[7,]    0    0    0    0    0    0    1

Look at the last one! It’s the identity matrix! Back to square one!

Or should I say square zero. If you multiplied again you would go through the cycle again. Likewise if you multiplied intermediate matrices from midway through, you would still travel around within the cycle. It would be exponent rules thing^x × thing^y = thing^[x+y] modulo 7.

What you’ve just discovered is the cyclic group P₇ (also sometimes called Z₇). The pair M.7, %*% is one way of presenting the only consistent multiplication table for 7 things. Another way of presenting the group is with the pair {0,1,2,3,4,5,6}, + mod 7 (that’s where it gets the name Z₇, because ℤ=the integers. A third way of presenting the cyclic 7-group, which we can also do in R:

> w <- complex( modulus=1, argument=2*pi/7 )
> w
[1] 0.6234898+0.7818315i
> w^2
[1] −0.2225209+0.9749279i
> w^3
[1] −0.9009689+0.4338837i
> w^4
[1] −0.9009689−0.4338837i
> w^5
[1] −0.2225209−0.9749279i
> w^6
[1] 0.6234898−0.7818315i
> w^7
[1] 1−0i

Whoa! All of a sudden at the 7th step we’re back to “1” again. (A different one, but “the unit element” nonetheless.)

So three different number systems—

• counting numbers;
• matrix-blocks; and
• a ring of imaginary numbers

— are all demonstrating the same underlying logic.

Although each is merely an idea with only a spiritual existence, these are the kinds of “logical atoms” that build up the theories we use to describe the actual world scientifically. (Counting = money, or demography, or forestry; matrix = classical mechanics, or video game visuals; imaginary numbers = electrical engineering, or quantum mechanics.)

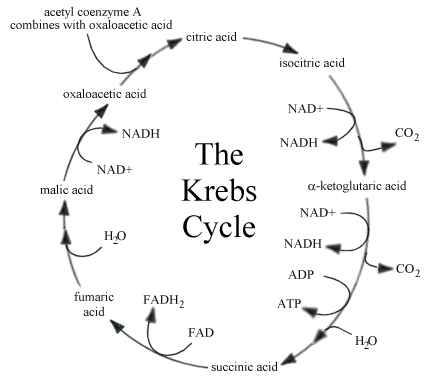
Three different number systems but they’re all essentially the same thing, which is this idea of a “cycle-of-7”. The cycle-of-7, when combined with other simple groups (also in matrix format), might model a biological system like a metabolic pathway.

Philosophically, P₇ is interesting because numbers—these existential things that seem to be around whether we think about them or not—have naturally formed into this “circular” shape. When a concept comes out of mathematics it feels more authoritative, a deep fact about the logical structure of the universe, perhaps closer to the root of all the mysteries.

In the real world I’d expect various other processes to hook into P₇—like a noise matrix, or some other groups. Other fundamental units should combine with it; I’d expect to see P₇ instantiated by itself rarely.

Mathematically, P₇ is interesting because three totally different number systems (imaginary, counting, square-matrix) are shown to have one “root cause” which is the group concept.

John Rhodes got famous for arguing that everything, but EVERYTHING, is built up from a logical structure made from SNAGs, of which P₇=C₇=Z₇ is one. viz, algebraic engineering

Or, in the words of Olaf Sporns:

[S]imple elements organize into dynamic patterns … Very different systems can generate strikingly similar patterns—for example, the motions of particles in a fluid or gas and the coordinated movements of bacterial colonies, swarms of fish, flocks of birds, or crowds of commuters returning home from work. … While looking for ways to compute voltage and current flow in electrical networks, the physicist Gustav Kirchhoff represented these networks as graphs…. [His] contemporary, Arthur Cayley, applied graph theoretical concepts to … enumerating chemical isomers….

Graphs, then, can be converted into adjacency matrices by putting a 0 where there is no connection between a and b in the [row=a, column=b], or putting a (±)1 where there is a (directed) link between the two nodes. The sparse [0’s, 1’s] matrix M.7 above is a transition matrix of the cyclical C₇ picture: 1 → 2 → 3 → 4 → 5 …. A noun (C₇) converted into a verb (%*% M.7).

In short, groups are one of those things that make people think: Hey, man, maybe EVERYTHING is a matrix. I’m going to go meditate on that.